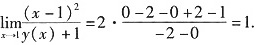问题
填空题
设y=y(x)是由方程y2+xy+x2-x=0确定的满足y(1)=-1的连续函数,则极限
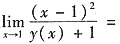 ______.
______.
答案
参考答案:A
解析:[考点] 隐函数求导,极限
由隐函数存在定理,由方程y2+xy+x2-x=0确定的满足y(1)=-1的连续函数y=y(x)在x=1的邻域内必可导. 对方程两边求导后,有:
2yy′+y+xy′+2x-1=0. 故
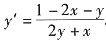 .
.
于是
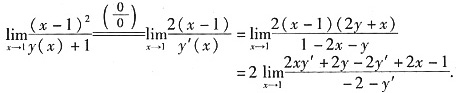
注意到
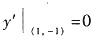 ,故
,故
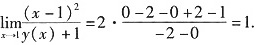
设y=y(x)是由方程y2+xy+x2-x=0确定的满足y(1)=-1的连续函数,则极限
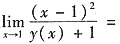 ______.
______.
参考答案:A
解析:[考点] 隐函数求导,极限
由隐函数存在定理,由方程y2+xy+x2-x=0确定的满足y(1)=-1的连续函数y=y(x)在x=1的邻域内必可导. 对方程两边求导后,有:
2yy′+y+xy′+2x-1=0. 故
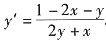 .
.
于是
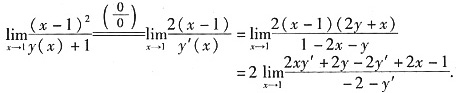
注意到
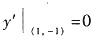 ,故
,故