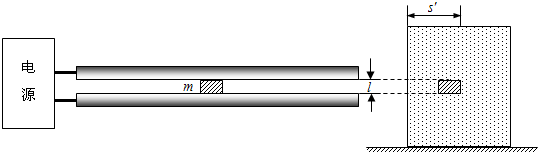
图是导轨式电磁炮实验装置示意图.两根平行长直金属导轨沿水平方向固定,其间安放金属滑块(即实验用弹丸).滑块可沿导轨无摩擦滑行,且始终与导轨保持良好接触.电源提供的强大电流从一根导轨流入,经过滑块,再从另一导轨流回电源.滑块被导轨中的电流形成的磁场推动而发射.在发射过程中,该磁场在滑块所在位置始终可以简化为匀强磁场,方向垂直于纸面,其强度与电流的关系为B=kI,比例常量k=2.5×10-6T/A.已知两导轨内侧间距l=1.5cm,滑块的质量m=30g,滑块沿导轨滑行5m后获得的发射速度v=3.0km/s(此过程视为匀加速运动).
(1)求发射过程中电源提供的电流强度.
(2)若电源输出的能量有4%转换为滑块的动能,则发射过程中电源的输出功率和输出电压各是多大?
(3)若此滑块射出后随即以速度v沿水平方向击中放在水平面上的砂箱,它嵌入砂箱的深度为s′.设砂箱质量为M,滑块质量为m,不计砂箱与水平面之间的摩擦.求滑块对砂箱平均冲击力的表达式.
(1)由匀加速运动公式 a=
=9×105m/s2v2 2s
由安培力公式和牛顿第二定律,有
F=IBl=kI2l
F=ma
因此
I=
=8.5×105Ama kl
即发射过程中电源提供的电流强度为8.5×105A.
(2)滑块获得的动能是电源输出能量的4%,即:P△t×4%=
mv21 2
发射过程中电源供电时间
△t=
=v a
×10-2s1 3
因而,所需的电源输出功率为
P=
=1.0×109W
mv21 2 △t×4%
由功率P=IU,解得输出电压:
U=
=1.2×103VP I
即发射过程中电源的输出功率为1.0×109W、输出电压为1.2×103V.
(3)分别对砂箱和滑块用动能定理,有
fsM=
MV2 1 2
f'sm=
mV2-1 2
mv21 2
由牛顿定律f=-f'和相对运动sm=sM+s'
再由动量守恒定律
mv=(m+M)V
联立求得
fs'=
•M m+M
mv21 2
故平均冲击力
f=
•M 2(m+M) v2 s′
即滑块对砂箱平均冲击力为M 2(m+M)
.v2 s′
