问题
解答题
已知函数y=(2m+1)x +m-3。
(1)若函数的图象是经过原点的直线,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
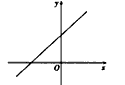
(3)若这个函数是一次函数且图象经过第一、二、三象限,求m的取值范围;
(4)若函数的图象和直线y=5x-3平行,求m的值;
(5)若函数图象与y轴的交点在y轴的正半轴,求m的取值范围。
答案
解:(1)因为图象过原点,所以m-3=0,即m=3;
(2)因为一次函数y随着x增大而减小,所以2m+1<0,解得m<-0.5;
(3)画出草图:可知k>0,b>0,即m+1>0,m-3>0,解得m>3;
(4)因为图象与直线y=5x-3平行,所以2m+1=5,解得m=2;
(5)因为函数图象与y轴的交点在y轴的正半轴,所以m-3>0,解得m>3。