对于数列A:a1,a2,…,an,若满足ai∈{0,1}(i=1,2,3,…,n),则称数列A为“0-1数列”。定义变换T,T将"0-1数列"A中原有的每个1都变成0,1,原有的每个0都变成1,0;例如A:1,0,1,则T(A):0,1,1,0,0,1。设A0是"0-1数列",令Ak=T(Ak-1),k=1,2,3,…,
(Ⅰ)若数列A2:1,0,0,1,0,1,1,0,1,0,0,1,求数列A1,A0;
(Ⅱ)若数列A0共有10项,则数列A2中连续两项相等的数对至少有多少对?请说明理由;
(Ⅲ)若A0为0,1,记数列Ak中连续两项都是0的数对个数为lk,k=1,2,3,…,求lk关于k的表达式。
解:(Ⅰ)由变换T的定义可得A1:0,1,1,0,0,1;
A0:1,0,1;
(Ⅱ)数列A0中连续两项相等的数对至少有10对;
证明:对于任意一个“0-1数列”A0,A0中每一个1在A2中对应连续四项1,0,0,1,在A0中每一个0在A2中对应的连续四项为0,1,1,0,
因此,共有10项的“0-1数列”A0中的每一个项在A2中都会对应一个连续相等的数对,
所以A2中至少有10对连续相等的数对。
(Ⅲ) 设Ak中有bk个01数对,
Ak+1中的00数对只能由Ak中的01数对得到,所以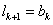 ,
,
Ak+1中的01数对有两个产生途径:①由Ak中的1得到;②由Ak中00得到,
由变换T的定义及A0:0,1可得Ak中0和1的个数总相等,且共有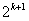 个,
个,
所以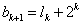 ,
,
所以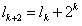 ,
,
由A0:0,1可得A1:1,0,0,1,A2:0,1,1,0,1,0,0,1,
所以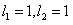 ;
;
当k≥3时,
若k为偶数,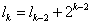 ,
,
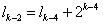 ,
,
…
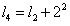 ,
,
上述各式相加可得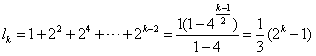 ,
,
经检验,k=2时,也满足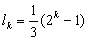 ;
;
若k为奇数,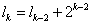 ,
,
 ,
,
…
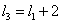 ,
,
上述各式相加可得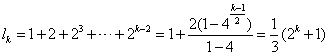 ,
,
经检验,k=1时,也满足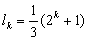 ;
;
所以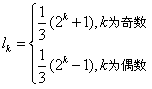 。
。
