问题
问答题
设f(x)、g(x)在[-a,a]上连续,g(x)为偶函数,且f(x)满足条件f(x)+f(-x)=A(A为常数).
(1) 证明
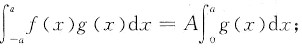
(2) 利用(1)的结论计算定积分

答案
参考答案:(1) [*]
又[*]
因此[*]
[*]
(2) 取f(x)=arctanex,g(x)=|sinx|,[*],则f(x),g(x)在[*]上连续,g(x)为偶函数,由[*]
知arctanex+arctane-x为常数,取x=0得,
[*]
所以[*],于是由(1)有
[*]
[评注] 对称区间上的定积分有下列重要结论:
[*]
解析:[考点提示] 对称区间上的定积分[*]一般分解为
[*]
再对第一个积分作变换x=-t即可.
