问题
解答题
已知{an}是由非负整数组成的数列，满足a1=0，a2=3，an+1an=（an-1+2）（an-2+2），n=3，4，5，……，
（1）求a3；
（2）证明an=an-2+2，n=3，4，5，……；
（3）求{an}的通项公式及其前n项和Sn。
答案
解：（1）由题设得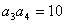
，且
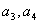均为非负整数，所以a3的可能的值为1、2、5、10，
若a3=1，则a4=10，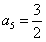
，与题设矛盾；
若a3=5，则a4=2，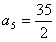
，与题设矛盾；
若a3=10，则a4=1，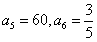
，与题设矛盾；
所以a3=2；
（2）用数学归纳法证明：
①当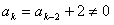
，等式成立；
②假设当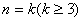
时等式成立，即
，
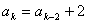由题设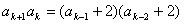
，
因为，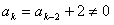
所以
，
也就是说，当n=k+1时，等式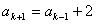
成立。
根据①②，对于所有n≥3，有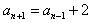
。
（3）由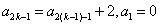
及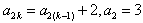
得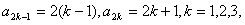
……，
即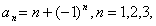
……，
所以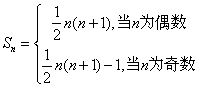
。