问题
解答题
已知数列{an}满足a1=0,a2=2,且对任意m,n∈N*都有a2m-1+a2n-1=2am+n-1+2(m-n)2,
(Ⅰ)求a3,a5;
(Ⅱ)设bn=a2n+1-a2n-1(n∈N*),证明:{bn}是等差数列;
(Ⅲ)设cn=(an+1-an)qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn。
答案
解:(Ⅰ)由题意,令m=2,n=1可得a3=2a2-a1+2=6,
再令m=3,n=1可得a5=2a3-a1+8=20.
(Ⅱ)当n∈N*时,由已知(以n+2代替m)可得a2n+3+a2n-1=2a2n+1+8,
于是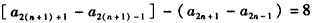 ,即
,即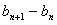 =8,
=8,
所以,数列{bn}是公差为8的等差数列.
(Ⅲ)由(Ⅰ)、(Ⅱ)的解答可知{bn}是首项b1=a3-a1=6,公差为8的等差数列,
则bn=8n-2,即a2n+1-a2n-1=8n-2,
另由已知(令m=1)可得,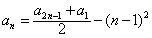 ,
,
那么,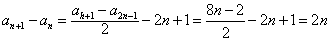 ,
,
于是,cn=2nqn-1,
当q=1时,Sn=2+4+6+…+2n=n(n+1);
当q≠1时,Sn=2·q0+4·q1+6·q2+…+2n·qn-1,
两边同乘q可得qSn=2·q1+4·q2+6·q3+…+2(n-1)·qn-1+2n·qn,
上述两式相减即得
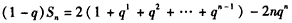
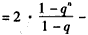
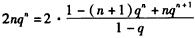 ,
,
所以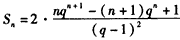 ,
,
综上所述,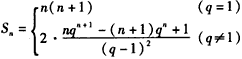 。
。
