问题
解答题
已知数列{an}的通项公式为an=n2-5n+4。
(1)数列中有多少项是负数?
(2)n为何值时,an有最小值?并求出最小值。
答案
解:(1)由n2-5n+4<0,解得1<n<4
∵n∈N*,
∴n=2,3
∴数列中有两项a2,a3是负数。
(2)∵an=n2-5n+4=(n- )2-
)2-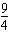 的对称轴方程为n=
的对称轴方程为n=
又n∈N*,∴n=2或n=3时,an有最小值,
其最小值为a2=a3=-2。
已知数列{an}的通项公式为an=n2-5n+4。
(1)数列中有多少项是负数?
(2)n为何值时,an有最小值?并求出最小值。
解:(1)由n2-5n+4<0,解得1<n<4
∵n∈N*,
∴n=2,3
∴数列中有两项a2,a3是负数。
(2)∵an=n2-5n+4=(n- )2-
)2-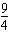 的对称轴方程为n=
的对称轴方程为n=
又n∈N*,∴n=2或n=3时,an有最小值,
其最小值为a2=a3=-2。