问题
解答题
求证:在直角三角形中,如果有一个锐角等于30°,那么这个锐角所对的直角边等于斜边的一半
答案
证明见解析
证明:延长AB到D,使BD=AB,连接CD
∵∠ABC=90°,∠BCA=30°∴∠BAC=60°
∵AC=DC ∴∠BDC=∠BAC=60° ∠BDC=60°
∵∠BDC=∠ACD ∴AC=AD ∴AB=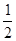 AD=
AD=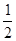 AC
AC
借助等边三角形的判定和性质证明
求证:在直角三角形中,如果有一个锐角等于30°,那么这个锐角所对的直角边等于斜边的一半
证明见解析
证明:延长AB到D,使BD=AB,连接CD
∵∠ABC=90°,∠BCA=30°∴∠BAC=60°
∵AC=DC ∴∠BDC=∠BAC=60° ∠BDC=60°
∵∠BDC=∠ACD ∴AC=AD ∴AB=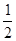 AD=
AD=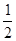 AC
AC
借助等边三角形的判定和性质证明