问题
问答题
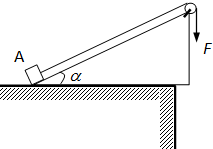
物块A静止在光滑斜面的底端,斜面倾角α=30°,斜面的长为l=1m,斜面固定在水平桌面上.用轻绳跨过斜面顶端的轻滑轮与物块A连接,滑轮与转轴之间的摩擦不计,开始绳刚好绷直,如图所示.若在绳的末端施一竖直向下的恒力F=7N拉绳,物块A由斜面底端到顶端经历的时间为1s.取重力加速度g=10m/s2.
(1)物块A的质量mA是多大?
(2)若物块A静止在斜面底端时,在绳的末端绕过定滑轮挂一重为GB=15N的物块,A物块经多长时间到达顶端?
答案
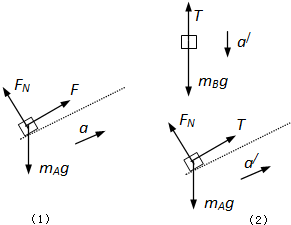
(1)对物块A受力分析如图
由牛顿第二定律F-mAgsin30°=mAa…①
由运动学公式l=
at2…②1 2
F=7N,l=1m,t=1s代入①②两式,解得
mA=1kg…③
(2)物块B的质量为mB=1.5kg,设绳中拉力为T,
物块A的加速度大小为a',
对物块B:GB-T=mBa'…④
对物块A:T-mAsin30°=mAa'…⑤
④⑤两式联列,解得:a'=4m/s2…⑥
设物块A从底端到顶端所用时间为t',
由运动学公式:l=
a′t′2,1 2
解得:t'=0.7s(或
s)2 2
答:(1)物块A的质量mA是1kg;
(2)A物块经0.7s时间到达顶端.
