问题
问答题
设二次型
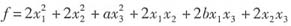经过正交变换X=QY化为标准形f=
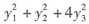，求参数a，b及正交矩阵Q。
答案
参考答案：二次型
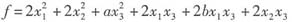的矩阵形式为f=XTAX，其中
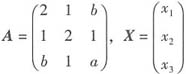，因为
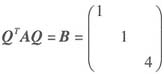，所以A～B(因为正交矩阵的转置矩阵即为其逆矩阵)，于是A的特征值为1，1，4，而|λE-A|=λ3-(a+4)λ2+(4a-b2+2)λ+(-3a-2b+2b2+2)，所以有λ3-(a+4)λ2+(4a-b2+2)λ+(-3a-2b+2b2+2)=(λ-1)2(λ-4)，解得a=2，b=1，当λ1=λ2=1时，由(E-A)X=0，得
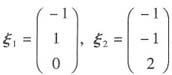，由λ3=4时，由(4E-A)X=0得
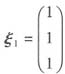，显然ξ1，ξ2，ξ3两两正交，单位化为
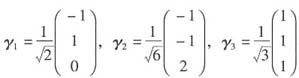，则
。
解析：[考点] 二次型及其标准型