问题
问答题
电动机通过一质量不计的绳子从静止开始吊起质量为8kg的物体,在前2s内绳的拉力恒定,此后电动机一直以最大的输出功率工作,物体被提升到90m高度时恰开始以15m/s的速度匀速上升.如图所示为上述过程的v-t图.试求:
(1)前2s内绳的拉力大小为多少?
(2)电动机的最大输出功率为多少?
(3)物体从静止开始被提升90m所需时间为多少?
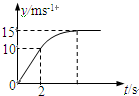
答案
(1)前2s内匀加速直线运动,a=
=△v △t
m/s2=5 m/s210 2
根据牛顿第二定律,有:ma=Fm-mg
解得Fm=ma+mg=(8×5+8×10)N=120N
(2)2s时刻电动机功率最大 Pm=Fmv1=120×10W=1200W
(3)前2秒位移:s1=
v1t1=1 2
×10×2m=10m;1 2
前90m过程,根据动能定理,有:
mv22-0=Fms1+Pt2-mgs,1 2
带入数据:
×8×152=120×10+1200×(t-2)-8×10×90,1 2
解得t=7.75s
答:(1)前2s内绳的拉力大小为120N;
(2)电动机的最大输出功率为1200W;
(3)物体从静止开始被提升90m所需时间为7.75s.
