问题
解答题
在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4psinθ+a=0相切，求实数a的值。
答案
解：将极坐标方程化为直角坐标方程，得圆的方程为x2+y2=2x，即（x-1）2 +y2=1，
直线的方程为3x+4y+a=0，
由题设知，圆心(1，0)到直线的距离为1，
即有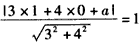
，解得a=-8或a=2，
故a的值为-8或2。
搜题请搜索小程序“爱下问搜题”
在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4psinθ+a=0相切，求实数a的值。
解：将极坐标方程化为直角坐标方程，得圆的方程为x2+y2=2x，即（x-1）2 +y2=1，
直线的方程为3x+4y+a=0，
由题设知，圆心(1，0)到直线的距离为1，
即有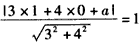，解得a=-8或a=2，
故a的值为-8或2。