问题
解答题
已知数列{an}的前n项和Sn=2an-2n,
(Ⅰ)求a3、a4;
(Ⅱ)证明:数列{an+1-2an}是一个等比数列;
(Ⅲ)求{an}的通项公式。
答案
解:(Ⅰ)因为Sn=2an-2n,
所以a1=2,S1=2,
由2an=Sn+2n,得
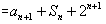 ,
,
得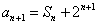 ,
,
所以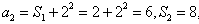 ,
,
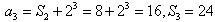 ,
,
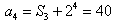 。
。
(Ⅱ)由题设和①式知
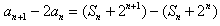
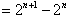
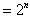 ,
,
所以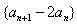 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
(Ⅲ)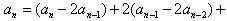 …+
…+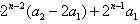 =(n+1)·2n-1。
=(n+1)·2n-1。
已知数列{an}的前n项和Sn=2an-2n,
(Ⅰ)求a3、a4;
(Ⅱ)证明:数列{an+1-2an}是一个等比数列;
(Ⅲ)求{an}的通项公式。
解:(Ⅰ)因为Sn=2an-2n,
所以a1=2,S1=2,
由2an=Sn+2n,得
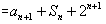 ,
,
得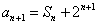 ,
,
所以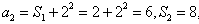 ,
,
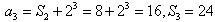 ,
,
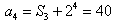 。
。
(Ⅱ)由题设和①式知
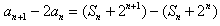
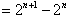
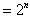 ,
,
所以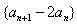 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
(Ⅲ)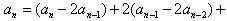 …+
…+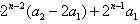 =(n+1)·2n-1。
=(n+1)·2n-1。