问题
解答题
已知：抛物线y=ax2+2x+c，对称轴为直线x=-1，抛物线与y轴交于点C，与轴交于A（-3，0）、B两点。 （1）求直线AC的解析式；
（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
（3）P为抛物线上一点，若以线段PB为直径的圆与直线BC切于点B，求点P的坐标。
答案
解：（1）∵对称轴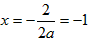
，
∴a=1，
∵A（-3，0），
∴c=-3，
设直线AC的解析式为y=kx+b，
∵A（-3，0），C（0，-3），
代入得：直线AC的解析式为y=-x-3；
（2）过点D作DM∥y轴分别交线段AC和x轴于点M、N，
设D（x，x2+2x-3），则M（x，-x-3），
∵S四边形ABCD=S△ABC+S△ACD=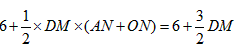
=
=
=
，
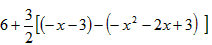
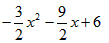
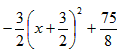∴当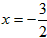
时，四边形ABCD面积有最大值
；
（3）如如图所示，由抛物线的轴对称性可求得B（1，0），
∵以线段PB为直径的圆与直线BC切于点B，
∴过点B作BC的垂线交抛物线于一点，则此点必为点P，
过点P作PE⊥x轴于点E，
可证Rt△PEB∽Rt△BOC，
∴
，
故EB=3PE，设P（x，x2+2x-3），
∵B（1，0），
∴BE=1-x，PE=x2+2x-31-x=3（x2+2x-3），
解得x1=1（不合题意舍去），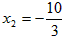
，
∴P点的坐标为：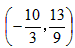
。
