问题
解答题
已知数列{an}中,a1=1,Sn是数列{an}的前n项和,且对任意n∈N*,有an+1=kSn+1(k为常数),
(Ⅰ)当k=2时,求a2,a3的值;
(Ⅱ)试判断数列{an}是否为等比数列?请说明理由。
答案
解:(Ⅰ)当k=2时,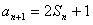 ,
,
令n=1得a2=2S1+1,
又a1=S1=1,得a2=3;
令n=2得a3=2S2+1=2(a1+a2)+1=9,∴a3=9,
∴a2=3,a3=9;
(Ⅱ)由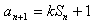 ,得
,得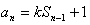 ,
,
两式相减,得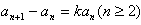 ,
,
即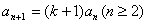 ,且
,且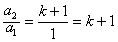 ,
,
故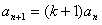 ,
,
故当k=-1时,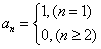 ,此时,{an}不是等比数列;
,此时,{an}不是等比数列;
当k≠-1时,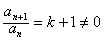 ,
,
此时,{an}是首项为1,公比为k+1的等比数列;
综上,当k=-1时,{an}不是等比数列;当k≠-1时,{an}是等比数列。
