在数1和100之间插入n个实数，使得这n+2个数构成递增的等比数列，

问题解答题

在数1和100之间插入n个实数，使得这n+2个数构成递增的等比数列，将这n+2个数的乘积记作T_n，再令a_n=lgT_n，n≥1，

(1)求数列{a_n}的通项公式；

(2)设b_n=tana_n·tana_n+1，求数列{b_n}的前n项和S_n．

答案

解：(1)设t₁，t₂，…，t_n+2构成等比数列，其中t₁=1，t_n+2=100，

则T_n=t₁·t₂·…·t_n+1·t_n+2， ①

T_n=t_n+2·t_n+1·…·t₂·t₁，②

①×②并用利t_it_n+3-i=t₁t_n+2=10²(1≤i≤n+2)，

得T_n²=(t₁t_n+2)·(t₂t_n+1)·…·(t_n+1t₂)·(t_n+2t₁)=10²⁽ⁿ⁺²⁾，

∴a_n=lgT_n=n+2，n≥1。

(2)由题意和(1)中计算结果，知b_n=tan (n+2)·tan(n+3)，n≥1，

另一方面，利用，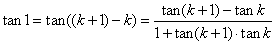

得，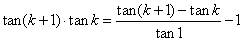

所以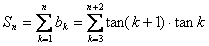

。
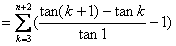
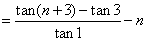