问题
单项选择题
设f(x)=3x3+x2|x|,则使f(n)(0)存在的最高阶数n为()。
A.0
B.1
C.2
D.3
答案
参考答案:C
解析:
[考点] 分段函数的高阶导数
3x3处处任意阶可导,只需考查φ(x)=x2|x|,它是分段函数,x=0是连接点.
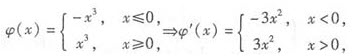
又φ’+(0)=(-x3)’+|x=0=0,φ’-(0)=(-x3)’-|x=0=0 φ’(0)=0;
φ’(0)=0;
同理可得

 φ’"(0)不存在,应选(C).
φ’"(0)不存在,应选(C).
设f(x)=3x3+x2|x|,则使f(n)(0)存在的最高阶数n为()。
A.0
B.1
C.2
D.3
参考答案:C
解析:
[考点] 分段函数的高阶导数
3x3处处任意阶可导,只需考查φ(x)=x2|x|,它是分段函数,x=0是连接点.
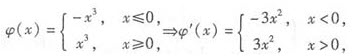
又φ’+(0)=(-x3)’+|x=0=0,φ’-(0)=(-x3)’-|x=0=0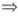 φ’(0)=0;
φ’(0)=0;
同理可得

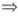 φ’"(0)不存在,应选(C).
φ’"(0)不存在,应选(C).