阅读理解。
Learning English is not easy. Almost every beginner of English asks himself: can I really learn to
communicate fluently (流利的) in English?
The answer is "yes"! According to some studies, almost anyone can learn a foreign language if he
or she wants to. Some might pick it up faster and some slower, but with the right methods and the
right attitude, almost anyone can succeed.
Successful English students usually have a positive attitude towards their studies. For example, they
are not afraid of making mistakes in front of others. They enjoy talking with people, even in bad English.
They enjoy singing English songs or watching English movies, even though they may not understand
exactly what they mean or are about. 他们努力永不放弃(A). Please believe there is no short cut to
learning a foreign language.
Many students also have their own special methods for studying English(B). Maybe you al-so have
some ideas of your own on how best to pick up English. Why not share them with your classmates?
Everyone has his own ways of learning so you should try to discover new ways. When you do, you
will find that studying English can be fun. You might even fall in love with it.
判断正(T)误(F)。
( )1. All beginners of English ask themselves: can I really learn to communicate fluently (流利的) in
English.
( )2. Successful English students usually are not afraid of making mistakes in front of others.
3. 把(A)处画横线的句子译为英语。
_________________________________________________________________________________
4. 把(B)处画横线的句子译为汉语。
_________________________________________________________________________________
5. What is the main idea of the passage?
_________________________________________________________________________________
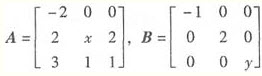 。
。 ,
, ,满足P-1AP=B.
,满足P-1AP=B.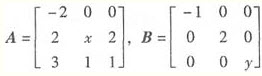 。
。 ,
, ,满足P-1AP=B.
,满足P-1AP=B.