问题
问答题
已知连续函数f(x)满足条件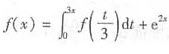 ,求f(x)。
,求f(x)。
答案
参考答案:
方程 两边对x求导得f’(x)=3f(x)+2e2x,即f’(x)-3f(x)=2e2x,令x=0,由原方程得f(0)=1.
两边对x求导得f’(x)=3f(x)+2e2x,即f’(x)-3f(x)=2e2x,令x=0,由原方程得f(0)=1.
于是,原问题就转化为求微分方程f’(x)-3f(x)=2e2x满足初始条件f(0)=1的特解.由一阶线性微分方程的通解公式,得
f(x)=e∫3dx(2e2x·e-∫3dxdx+C)=e3x(∫2e-xdx+C)=Ce3x-2e2x.
代入初始条件f(0)=1,得C=3,从而f(x)=3e3x-2e2x.
解析:
[考点] 先在等式两边对x求导,消去变限积分,将原方程化为关于未知函数f(x)的微分方程,再求解该微分方程
