问题
问答题
设函数f（x）在[0，3]上连续，在（0，3）内可导，且f（0）+f（1）+f（2）=3，f（3）=1，试证必存在ξ∈（0，3），使f’（ξ）=0。
答案
参考答案：
由题设，f(x)在[0，3]上连续，则f(x)在[0，2]上也必然连续，则在[0，2]上f(x)必有最大值M和最小值m，因而m≤f(0)≤M，m≤f(1)≤M，m≤f(2)≤M，从而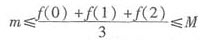
。
由连续函数的介值定理，知存在一点η∈[0，2]，使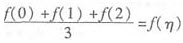
。
由已知条件f(0)+f(1)+f(2)=3，可推知f(η)=1，因此f(η)=f(3)=1，η∈[0，2]．
由罗尔定理，知存在ξ∈(η，3)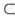
(0，3)，使f’(ξ)=0．证毕。
解析：
[考点] 介值定理、微分中值定理