B
“The Lord of the Rings”, one of the best sellers in the new millennium(千年), was made up of three parts——“The Fellowship of the Ring”, “Two Towers”, and “The Return of the King”. Millions upon millions of people have read it in over 25 different languages, but fewer know about the author and the history of the composition of the creative masterwork.
John Ronald Reuel Tolkien was born in South Africa in 1892. His parents died when he was a child. Living in England with his aunt, Tolkien and his cousins made up play languages, a hobby that led to Tolkien’s becoming skilled in Welsh, Greek, Gothic, Old Norse and Anglo-Saxon.
After graduating from Oxford, Tolkien served in World War I. In 1917, while recovering from trench fever, he began composing the mythology for The Rings. As a professor of Anglo-Saxon in 1930s at Oxford, Tolkien was part of an informal discussion group called the Inklings, which included several writers. The group was soon listening to chapters of Tolkien’s imaginative work “The Hobbit”.
Hobbit was a name Tolkien created for a local people that could best be described as half-sized members of the English rural(乡村的)class. Hobbits live in hillside holes. One of them, Bilbo Baggins, looks for treasures with a group of dwarves(侏儒). On the way, he meets the twisted, pitiful creature Gollum, from whom he sees a golden ring that makes the holder invisible(看不见的).
One of Tolkien’s students persuaded her employer, publisher Allen & Unwin, to look at a draft(草稿). The chairman of the firm, Stanley Unwin, thought that the best judge for a children’s book would be his ten-year-old son. The boy earned a shilling for reporting back that the adventure was exciting, and “The Hobbit” was published in 1937.
It sold so well that Unwin asked for a continuation. Over a dozen years later, in 1954, Tolkien produced “The Lord of the Rings”, a series of books so creative that they hold readers—new and old —after their publication.
54. Which of the following is true according to the passage?
A. “The Lord of the Rings” didn’t sell well in the last millennium.
B. People know better about Tolkien himself than about his works.
C. Tolkien was quite familiar with Old English.
D. Tolkien knew very well about different kinds of local languages in Africa.
55. What can we learn about “Hobbit” that Tolkien created in his works?
A. Hobbit was a race living in English downtown areas.
B. Hobbit was a local people who were very tall and strong.
C. Hobbit was a social group of people who lived in old castles.
D. Hobbit was a group of people who were mostly dwarves.
56. Which of the following shows the right order of Mr J.R.R.Tolkien’s life experience?
a. He had his “The Hobbit” published. b. He became a member of the Inklings.
c. He served in World WarⅠ d. He became an undergraduate at Oxford.
e. “The Lord of the Rings” came to the world. f. He moved to England to live with his aunt.
A. f-d-b-c-a-e B. f-d-c-b-a-e C. f-c-d-b-e-a D. d-f-c-a-b-e
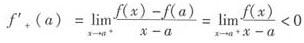 ,由极限的保号性知,存在δ>0,当x∈(a,a+δ)时,
,由极限的保号性知,存在δ>0,当x∈(a,a+δ)时,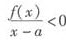 ,f(x)<0,取c∈(a,a+δ),则f(c)<0,f(x)在[c,b]上连续,又f(c)<0,f(b)>0,由零点定理知,存在ξ∈(c,b)
,f(x)<0,取c∈(a,a+δ),则f(c)<0,f(x)在[c,b]上连续,又f(c)<0,f(b)>0,由零点定理知,存在ξ∈(c,b)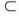 (a,b),使得f(ξ)=0。
(a,b),使得f(ξ)=0。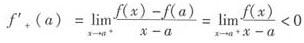 ,由极限的保号性知,存在δ>0,当x∈(a,a+δ)时,
,由极限的保号性知,存在δ>0,当x∈(a,a+δ)时,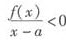 ,f(x)<0,取c∈(a,a+δ),则f(c)<0,f(x)在[c,b]上连续,又f(c)<0,f(b)>0,由零点定理知,存在ξ∈(c,b)
,f(x)<0,取c∈(a,a+δ),则f(c)<0,f(x)在[c,b]上连续,又f(c)<0,f(b)>0,由零点定理知,存在ξ∈(c,b)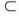 (a,b),使得f(ξ)=0。
(a,b),使得f(ξ)=0。