问题
单项选择题
设三阶矩阵A的特征值为-1，1，2，矩阵A与B相似，则下列矩阵可逆的是（）。
A．B+E
B．B-1+E
C．B*-E
D．B2-4E
答案
参考答案：C
解析：
[考点] 矩阵可逆的判断
由题意知，B的特征值也是-1，1，2，从而由|B|=-2≠0知，
B是可逆阵，且B*=|B|·B-1=-2B-1。据此，可知B2的特征值为1，1，4；B-1的特征值为-1，1，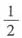
；B*的特征值为2，-2，-1，进而可知，B+E的特征值为0，2，3；B-1+E的特征值为0，2，
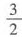；B*-E的特征值为1，-3，-2；B2-4E的特征值为-3，-3，0，
因为|B*-E|≠0，所以B*-E可逆，应选(C)。