参考答案：

由y(x)=e^-2xf(x，x)，有y’(x)=-2e^-2xf(x，x)+e^-2x[f’₁(x，x)+f’₂(x，x)]，

又条件f’_u(u，v)+f’_v(u，v)=sin(u+v)e^u+v，

即f’₁(u，v)+-f₂’(u，v)=sin(u+v)e^u+v，

令u=x，v=x得f₁’(x，x)+f₂’(x，x)=sin(2x)e^2x，

于是y(x)满足一阶线性微分方程y’(x)+2y(x)=sin2x。

通解为y(x)=e^-2x[∫sin2x·e^2xdx+c]，

由分部积分公式，可得

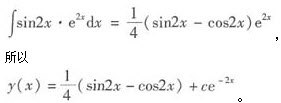
解析：

[考点] 微分方程的解