参考答案：

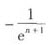
解析：

[考点] 先求n阶导数，再求极值

f(x)=xe^x

f⁽ⁿ⁾(x)=(n+x)e^x

f⁽ⁿ⁺¹⁾(x)=(n+1+x)e^x

f⁽ⁿ⁺²⁾(x)=(n+2+x)e^x

令f⁽ⁿ⁺¹⁾(x)=0，解得f⁽ⁿ⁾(x)的驻点x=-(n+1)，

又f⁽ⁿ⁺²⁾[-(n+1)]=[n+2-(n+1)]e^-(n+1)=e^-(n+1)＞0，

故x=-(n+1)为f⁽ⁿ⁾(x)的极小值点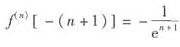，。