问题
填空题
设曲线
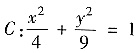 ,取逆时针方向,则
,取逆时针方向,则
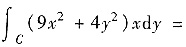 ______.
______.
答案
参考答案:216π.
解析:先用曲线方程化简被积函数:
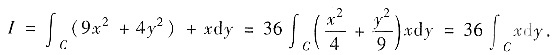
方法1°再用参数方程化为定积分:x=2cost,y=3sint,t∈[0,2π],则有
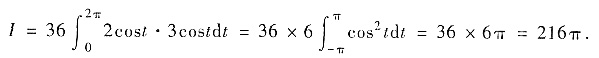
方法2°用格林公式. C围成区域D,则
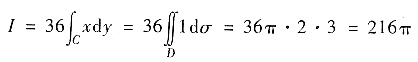
其中椭圆D的面积为6π.
①本题有如下变式:设曲线
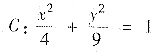 ,取逆时针方向,则
,取逆时针方向,则
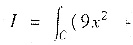 4y2)|y|dx=______.
4y2)|y|dx=______.
分析同样转化为求
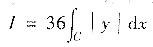
方法1°用C的参数方程化为定积分:x=2cost,y=3sint,t∈[0,2π],则有
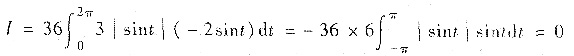
(周期函数与奇函数的积分性质)
方法2°为了去掉绝对值,把C分成两段:Ci(i=1,2),分别位于上半平面与下半平面,并配上坐标轴部分,分别构成闭曲线Li(i=1,2),均为逆时针方向,见下图
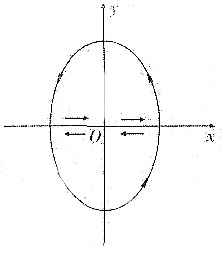
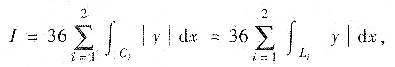
其中坐标轴部分取积分两次,但方向相反抵消了.
Li围成区域记为Di(i=1,2),它们的面积相等为3π. 在Di上用格林公式得
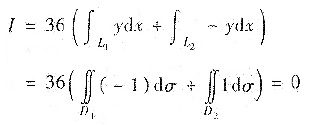
方法3°直接利用对称性.
C关于x轴对称,P(x,y)=|y|对y为偶数,则
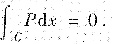
②注意第一、二类曲线积分有不同的对称性质,若熟悉,则利用它解此题最简便.
