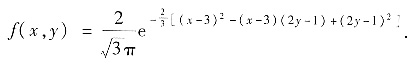问题
问答题
已知(X，Y)为一个二维随机变量，X1=X+2Y，X2=X-2Y. (X1，X2)的概率密度为f(x1，x2)
(Ⅰ)分别求出X和Y的密度函数；
(Ⅱ)求X和Y的相关系数，并由此写出(X，Y)的联合密度.
答案
参考答案：(Ⅰ)由(X1，X2)的联合密度可知X1与X2相互独立，且
X1～N(4，3)，X2～N(2，1)
由正态分布的性质可知，X1，X2的线性组合仍服从正态分布，而由
X1=X+2Y，X2=X-2Y
得
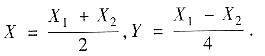
根据期望和方差的性质有
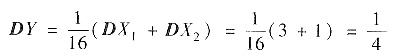
从而可知X～N(3，1)，
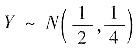
即
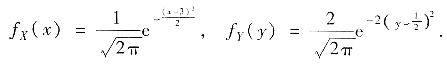
(Ⅱ)由X1=X+2Y可知，DX1=DX+4DY+4cov(X，Y)
故
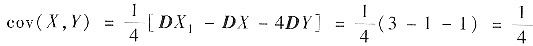
由二维正态分布密度函数
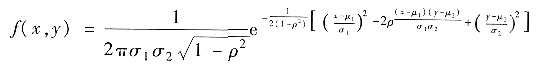
将
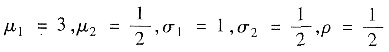代入上式中，可得
