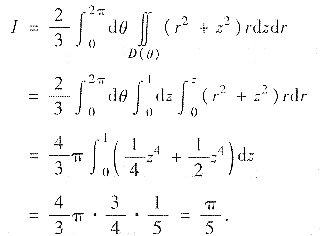问题
问答题
设密度为1的立体Ω由不等式
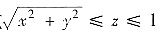 表示,试求Ω绕直线x=y=z的转动惯量.
表示,试求Ω绕直线x=y=z的转动惯量.
答案
参考答案:Ω上任意点(x,y,z)到直线L的距离的平方
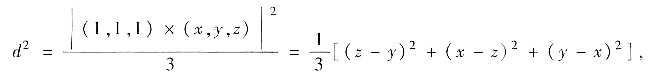
其中

再求Ω对L的转动惯量
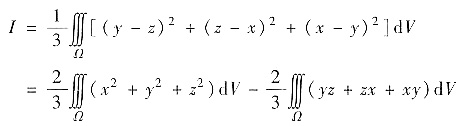
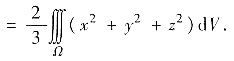 (对称区域上奇偶函数的积分性质)
(对称区域上奇偶函数的积分性质)
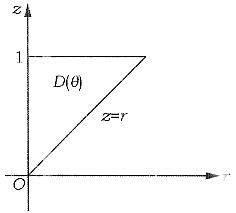
用先二后一的积分顺序,记D(z):x2+y2≤z2,于是
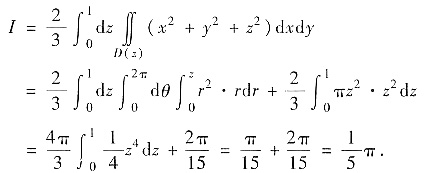
解析:质量为m的质点对直线L的转动惯量为md2,d是质点到L的距离. 因此,要先求Ω上
 点(x,y,z)到直线L:x=y=z的距离,然后用三重积分来表示这个转动惯量.
点(x,y,z)到直线L:x=y=z的距离,然后用三重积分来表示这个转动惯量.
若用柱坐标变换,并用先z的积分顺序得
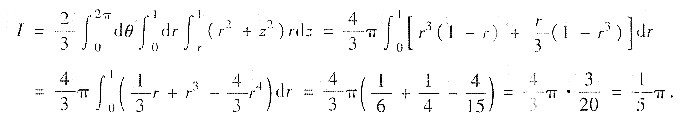
若用柱坐标变换,并用先r、z后θ的积分顺序得