问题
问答题
历史上科学家皮尔逊进行抛掷一枚匀称硬币的试验，他当时掷了12000次，正面出现6019次. 现在我们若重复他的试验，试求：
(Ⅰ)抛掷12000次正面出现频率与概率之差的绝对值不超过当年皮尔逊试验偏差的概率；
(Ⅱ)要想使我们试验正面出现的频率与概率之差的绝对值不超过皮尔逊试验偏差的概率小于20%，现在我们应最多试验多少次？
附：标准正态分布函数表：
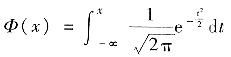
| x | 0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
| Φ(x) | 0.50 | 0.52 | 0.54 | 0.56 | 0.58 | 0.60 | 0.62 | 0.64 | 0.66 | 0.67 | 0.69 |
答案
参考答案：(Ⅰ)设X表示试验中正面出现的次数X～B(12000，0.5)，且EX=np=6000，DX=npq=3000. 由于n=12000相当大，因此
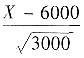近似服从正态分布N(0，1)，于是
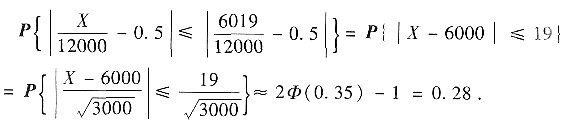
(Ⅱ)设至多试验n次，Y为n次中正面出现的次数’显然Y～B(n，0.5)，EY=0.5n，DY=0.25n，于是
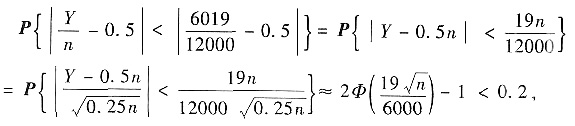
即
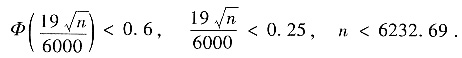
故最多试验6232次即可.