问题
问答题
设f(x,y)在全平面有三阶连续偏导数,并满足
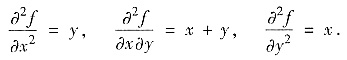
试求:(Ⅰ)
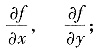 (Ⅱ)f(x,y).
(Ⅱ)f(x,y).
答案
参考答案:(Ⅰ)(Ⅰ)先求
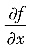 与
与
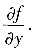
1°由
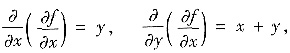 求
求
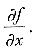
将第一式对x积分得
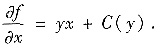
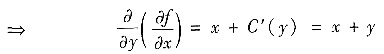
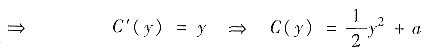 (以为
(以为
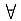 常数)
常数)
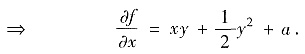
2°由
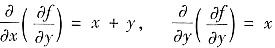 ,求
,求
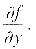
将第一式对x积分得
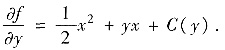

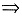 C(y)=b(b为
C(y)=b(b为
 常数)
常数)

(Ⅱ)由
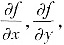 求f(x,y).
求f(x,y).
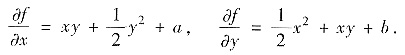
将第一式对x积分得
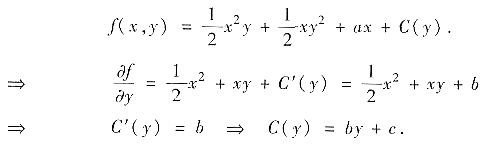
因此求得
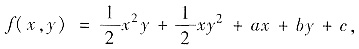 其中a,b,c为
其中a,b,c为
 常数.
常数.
解析:由给定的三个二阶偏导数

若熟悉z=f(x,y)的二阶泰勒公式,可直接求出f(x,y),即
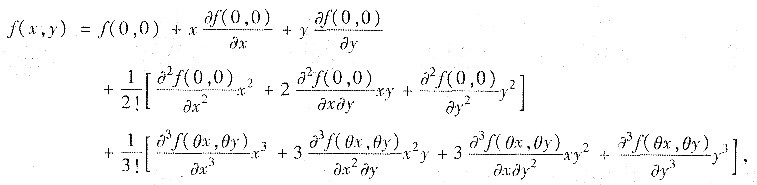
其中0<θ<1.
记f(0,0)=c,
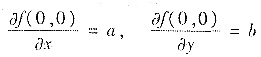 ,再注意f(x,y)各二阶偏导数在(0,0)的值均为零,各三阶偏导数为(*)式所指出的常数值,立即得
,再注意f(x,y)各二阶偏导数在(0,0)的值均为零,各三阶偏导数为(*)式所指出的常数值,立即得
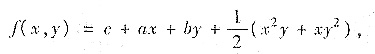
其中a,b,c为
 常数.
常数.