问题
单项选择题
设二维离散型随机变量(X,Y)的联合概率分布如下表所示
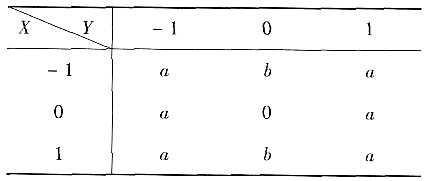
其中a>0,b>0,则一定有
A.X与Y不相关.
B.X2与Y2不相关.
C.X+Y与X-Y不相关.
D.X2+Y2与X2-Y2不相关.
答案
参考答案:A
解析:从题设条件可得
EX=EY=0,EXY=a-a-a+a=0,
cov(X,Y)=EXY-EXEY=0,ρ=0,
即X与Y不相关,故应选A.
进一步分析,X2与Y2的联合概率分布应为
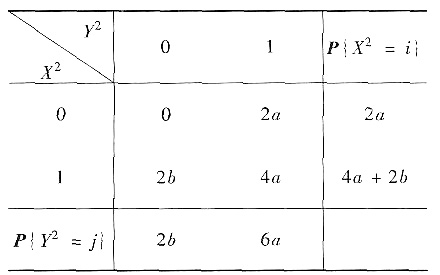
EX2=4a+2b,EY2=6a,EX2Y2=4a.
对于选项B:X2与Y2不相关
 EX2Y2=EY2EY2
EX2Y2=EY2EY2
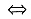 6a(4a+2b)=4a
6a(4a+2b)=4a
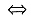 6a+3b=1,
6a+3b=1,
与6a+2b=1且b>0相矛盾,故选项B不成立.
对于选项C和D:X+Y与X-Y不相关
 cov(X+Y,X-Y)=0
cov(X+Y,X-Y)=0
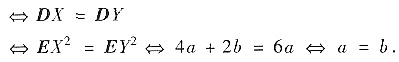
X2+Y2与X2-Y2不相关
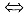 cov(X2+Y2,X2-Y2)=0
cov(X2+Y2,X2-Y2)=0
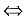 DX2=DY2
DX2=DY2
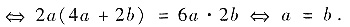
若令a=0.15,b=0.05,a≠b,则X+Y与X-Y相关且X2+Y2与X2-Y2也相关,故选项C与D均不成立.
