问题
填空题
| 若x1,x2∈R,x1≠x2,则下列性质对函数f(x)=2x成立的是______.(把满足条件的序号全部写在横线上) ①f(x1+x2)=f(x1)•f(x2)②f(x1•x2)=f(x1)+f(x2) ③[f(x1)-f(x2)]•(x1-x2)>0④f(x1)+f(x2)>2f(
|
答案
①f(x1+x2)=2x1+x2=2x1×2x2=f(x1)•f(x2)①对
②f(x1•x2)=2x1•x2,f(x1)+f(x2)=2x1+2x2,f(x1•x2)≠f(x1)+f(x2)②错
③f(x)在定义域R上是增函数,对于任意的两不等实数x1,x2,若x1>x2 则f(x1)>f(x2),若x1<x2 则f(x1)<f(x2),总之必有[f(x1)-f(x2)]•(x1-x2)>0.③对
④如图A,B为函数图象上任意不同两点,M为线段AB的中点,过M且与x轴垂直的直线与图象交与点P.各点坐标如图所示.
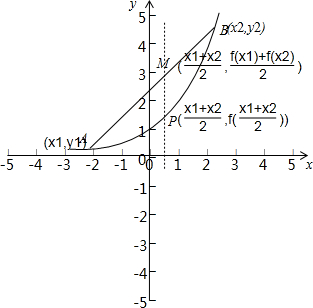
由图可知
>f(f(x1)+f(x2) 2
),两边同时乘以2,即知④对.x1+x2 2
故答案为:①③④.
