问题
解答题
(1)定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和。如果等和数列{an}的首项a1=a，公和为m，试归纳a2，a3，a4的值，猜想{an}的通项公式；
(2)类比“等和数列”猜想“等积数列”{bn}的首项b1=b，公积为p的通项公式；
(3)利用(1)和(2)探究是否存在一个数列既是“等和数列”；又是“等积数列”，并举例说明.
答案
解：（1）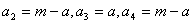
，
通项公式为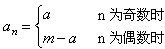
；
（2）等积数列的通项公式为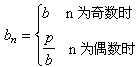
。
（3）由(1)和(2)一个数列既是“等和数列”；又是“等积数列”；必须奇数项相同即a=b，
同时偶数项也相同即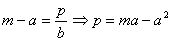
，
例如，不妨取a=b=1，则p=m-1，
即常数列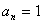
既是“等和数列”；又是“等积数列”。