问题
解答题
在数列{an}与{bn}中,a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项,n∈N*,
(Ⅰ)求a2,b2的值;
(Ⅱ)求数列{an}与{bn}的通项公式;
答案
解:(1)由题设有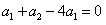 ,a1=1,解得
,a1=1,解得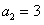 ,
,
由题设又有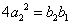 ,b1=4,解得
,b1=4,解得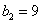 ;
;
(2)由题设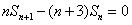 ,2an+1为bn与bn+1的等比中项,a1=1,b1=4,及
,2an+1为bn与bn+1的等比中项,a1=1,b1=4,及 ,
,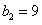 ,
,
进一步可得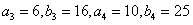 ,
,
猜想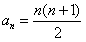 ,
,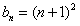 ,n∈N*,
,n∈N*,
先证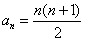 ,n∈N*,
,n∈N*,
当n=1时,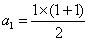 ,等式成立;
,等式成立;
当n≥2时用数学归纳法证明如下:
(1)当n=2时,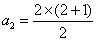 ,等式成立;
,等式成立;
(2)假设n=k时等式成立,即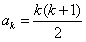 ,k≥2,
,k≥2,
由题设,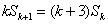 , ①
, ①
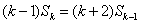 ,②
,②
①的两边分别减去②的两边,整理得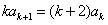 ,
,
从而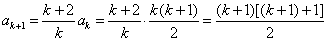 .
.
这就是说,当n=k+1时等式也成立.
根据(1)和(2)可知,等式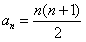 对任何的n≥2成立.
对任何的n≥2成立.
综上所述,等式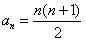 对任何的n∈N*都成立;
对任何的n∈N*都成立;
再用数学归纳法证明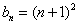 ,n∈N*。
,n∈N*。
(1)当n=1时,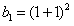 =4,等式成立;
=4,等式成立;
(2)假设当n=k时等式成立,
即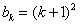 ,那么
,那么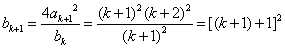 ,
,
这就是说,当n=k+1时等式也成立.
根据(1)和(2)可知,等式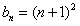 对任何的n∈N*都成立。
对任何的n∈N*都成立。
