问题
问答题
将一枚骰子独立地重复掷n次，以Sn表示各次掷出的点数之和．
(Ⅰ) 证明：当n→∞时，随机变量
的极限分布是标准正态分布；
(Ⅱ) 为使
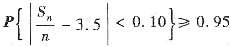，至少需要将骰子重复掷多少次
答案
参考答案：[证明与求解] (Ⅰ)设X1，X2，…，Xn表示将一枚骰子独立地重复掷n次各次掷出的点数，易见它们是独立同分布随机变量，且EXk=3.5(k=1，2，…，n)．不难计算其方差：
[*]
由于Sn=X1+X1+…+Xn，则[*]．因此根据列维-林德伯格中心极限定理，知当n→∞，随机变量
[*]
的极限分布是标准正态分布．
(Ⅱ) 掷骰子需要重复的次数n，满足下列关系式：
[*]
由此可见
[*]
于是为满足所给条件，至少需要将骰子重复掷1121次．
解析：
[*]