问题
问答题
设随机变量
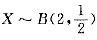和随机变量Y～N(0，1)，且X与Y相互独立．令
Z=(X-1)Y，记(Y，Z)的分布函数为F(y，z)．
求：(Ⅰ)Z的分布函数FZ(z)；
(Ⅱ)F(1，1)的值，已知
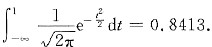
答案
参考答案：
Fz(z)=P{Z≤z}=P{(X-1)Y≤z}
=P{X=0}P{(X-1)Y≤z |X=0}+
P{X=1}P{(X-1)Y≤z|X=1}
+P{X=2}P{(X-1)Y≤z|X=2}
[*](Ⅱ)
[*]
解析：[*]
Y～N(0，1)，设标准正态分布的分布函数为φ(x)．
而Z=(X-1)Y是离散型与连续型随机变量之积，讨论Fz(z)=P{Z≤z}，可将X=0，1，2分情况讨论．
[*]
