问题
问答题
设二维连续型随机变量(X,Y)的联合概率密度为
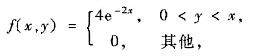
令随机变量U=-X,V=X+Y,
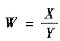 ,求:
,求:
(Ⅰ) U的分布函数F1(u);
(Ⅱ) V的分布函数F2(v);
(Ⅲ) W的分布函数F3(w);
(Ⅳ) U与W的联合分布函数F(u,w).
答案
参考答案:[解] (Ⅰ) 由于随机变量X只取正值,因此随机变量U=-X只取负值.当u<0时,
[*]
故U的分布函数F1(u)为
[*]
(Ⅱ) 当v<0时,F2(v)=0;当v≥0时,
[*]
故V的分布函数F2(v)为
[*]
(Ⅲ) 当w<1时,F3(w)=0;当w≥1时,
[*]
故W的分布函数F3(w)为
[*]
(Ⅳ) [*]
当w<1时,F(u,w)=0;当u<0,w≥1时,
[*]
当u≥0,w≥1时,
[*]
故U与W的联合分布函数F(u,w)为
[*]
解析:
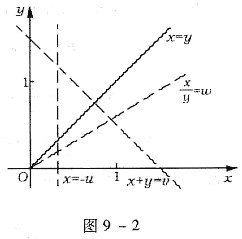
[分析]: 求随机变量及其函数的分布函数,就是计算有关随机事件的概率,对于连续型随机变量,若已知其联合概率密度f(x,y),计算(X,Y)在某一区域D内取值的概率就是计算一个二重积分:
[*]
[*]
