问题
问答题
已知(X,Y)的联合密度函数
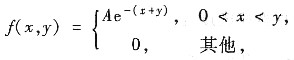
(Ⅰ) 求常数A;(X,Y)的联合分布函数F(x,y),并问X与Y是否独立为什么
(Ⅱ) 求条件概率密度fX|Y(x|y),fY|X(y|x)及条件概率
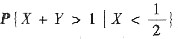 ;
;
(Ⅲ) 记Z1=Y-X,求证Z1服从参数λ=1的指数分布,并计算Z2=X+Y的概率密度.
答案
参考答案:[分析与解答]
[*]
[*]
[*]
因为 FX(x)·FY(y)≠F(x,y),所以X与Y不独立.
(Ⅱ) 由于X的概率密度
[*]
Y的概率密度
[*]
所以
[*]
条件概率
[*]
其中
[*]
[*]
故
[*]
(Ⅲ) 我们通过求Z1=Y-X的分布函数(或概率密度)来证明Z1服从参数λ=1的指数分布,有两种方法:
方法1° (分布函数法) Z1=Y-X的分布函数[*]
当z≤0时,F1(z)=0;当z>0时,
[*]的指数分布.
方法2°(公式法) 如果(X,Y)~f(x,y),则Z1=Y-X的概率密度
[*]
其中
[*]
[*]
由此可知:当z≤0时f1(z)=0;当z>0时[*]所以Z1=Y-X服从参数λ=1的指数分布.
仿照上述方法我们可以求得Z2=X+Y的概率密度f2(z).
方法1°(分布函数法) Z2=X+Y的分布函数
[*]
由f(x,y)的非零定义域知:当z≤0时F2(x)=0;当z>0时
[*]
综上得
[*]
方法2°(公式法) 若(X,Y)~f(x,y),则Z2=X+Y的概率密度
[*]
其中
[*]
所以当z≤0时f2(z)=0;当z>0时
[*]
综上得
[*]
[*]
解析:
[*]
