问题
单项选择题
下列结论正确的是
(A) 方阵A与其转置矩阵AT有相同的特征值，从而有相同的特征向量．
(B) 任意两个同阶的对角矩阵都可以相似于同一个对角矩阵．
(C) 对应于实矩阵的相异特征值的实特征向量必是正交的．
(D) 设PTAP=B，若A为正定矩阵，|P|≠0，则B必为正定矩阵．
答案
参考答案：D
解析： 对于(A)：由矩阵的特征值和特征向量的性质可知，方阵A与AT有相同的特征多项式，故A和AT有相同的特征值，但对应的特征向量不一定相同．例如：矩阵
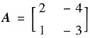与AT有相同的特征值1和-2，而A对应的特征向量是
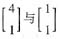，AT对应的特征向量是
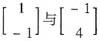．因此(A)不正确．
对于(B)：由“两个同阶但秩不相等的矩阵一定不相似于同一个对角矩阵”可知(B)不正确．要注意的是若矩阵B与A相似，即存在可逆矩阵P，满足P-1AP=B，这实际上也是矩阵A经若干次初等行变换和初等列变换而成为矩阵B的．而初等变换不改变矩阵的秩，即等价矩阵的秩相同，所以相似矩阵当然也是等价矩阵，也具有相同的秩．例如，对应于实矩阵
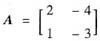的两个相异特征值1和-2的实特征向量
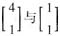不是正交的．
注意，实对称矩阵与实矩阵的区别：不同的特征值对应的特征向量是正交的，此乃实对称矩阵具有的性质，而实矩阵不同的特征值对应的特征向量是线性无关的．
对于(D)：由“与正定矩阵合同的矩阵必定是正定矩阵”可知(D)正确．
事实上，这是两个矩阵合同具有的性质．合同矩阵除了等价、具有相同的秩外，还具有相同的正惯性指数，故正定性相同．