问题
单项选择题
设n阶矩阵A可逆，α是A的属于特征值A的特征向量，则下列结论中不正确的是
(A) α是矩阵-2A的属于特征值-2λ的特征向量．
(B) α是矩阵
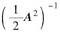的属于特征值
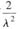的特征向量．
(C) α是矩阵A*的属于特征值上
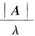的特征向量．
(D) α是矩阵P-1A的属于特征值A的特征向量，其中P为n阶可逆矩阵．
答案
参考答案：D
解析： 由Aα=λα(α≠0)，可得
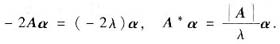
又
，两边左乘
，可得
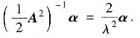
由此可知，(A)，(B)，(C)均正确，应选(D)．
事实上，由Aα=λα可得(P-1A)α=A(P-1α)，即P-1α是矩阵P-1A的属于特征值λ的特征向量．