问题
填空题
若二次型f(x1，x2，x3)=
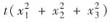-4x1x2-4x1x3+4x2x3是正定的，则t的取值范围是
答案
参考答案：t＞2
解析： 二次型的矩阵为
，可求得A的各阶顺序主子式
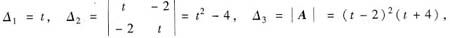
由△1＞0得t＞0；由△2＞0得t＞2或t＜-2；由△3＞0得t＞-4．故当t＞2时，有△1＞0，△2>0，△3＞0，A为正定矩阵，从而f为正定的二次型．
搜题请搜索小程序“爱下问搜题”
若二次型f(x1，x2，x3)=
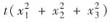-4x1x2-4x1x3+4x2x3是正定的，则t的取值范围是
参考答案：t＞2
解析： 二次型的矩阵为
，可求得A的各阶顺序主子式
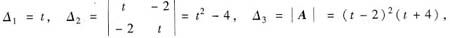
由△1＞0得t＞0；由△2＞0得t＞2或t＜-2；由△3＞0得t＞-4．故当t＞2时，有△1＞0，△2>0，△3＞0，A为正定矩阵，从而f为正定的二次型．