问题
单项选择题
设A为n阶矩阵,则在下列条件中,不是“A的特征值为-1”的充分条件的是
(A) A2=E. (B) r(A+E)<n.
(C) A的各行元素之和均为-1. (D) AT=-A,且1是A的特征值.
答案
参考答案:A
解析: 对于选项(A):由于A2=E,故A的特征值是1或-1,但-1不一定是A的特征值.例如,A=E,A2=E,但-1不是A的特征值.因此,应该选(A).
对于(B),(C),(D):若r(A+E)<n,则|A+E|=0,A的特征值为-1;若A的各行元素之和均为-1,则有
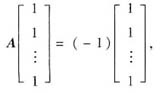
即A的特征值为-1.若AT=-A,1是A的特征值,则|E-A|=|(E-A)T|=|E-AT|=|E+A|=0,即A的特征值为-1.因此,(B),(C),(D)均是充分条件,应该排除.
