问题
单项选择题
设A，B为n阶矩阵，则A与B相似的充分必要条件是
(A) A，B都相似于对角矩阵． (B) |λE-A|=|λE-B|．
(C) 存在正交矩阵Q，使得Q-1AQ=B． (D) 存在可逆矩阵P，使得ABT=PTB．
答案
参考答案：D
解析： A～B
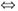存在可逆矩阵P1，使得
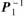AP1=B
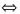存在可逆矩阵
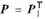，使得(PT)-1APT=B
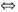存在可逆矩阵P，使得APT=PTB．故应选(D)．
由于A～B，不一定A，B都相似于对角矩阵，故(A)不对．
|λE-A|=|λE-E|是A～B的必要条件，但不是充分条件，例如：矩阵
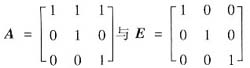
有相同的特征多项式为(λ-1)3，但A与B不是相似矩阵，因为对任何可逆矩阵P使P-1AP=E，有A=PEP-1=E，而A≠E．故(B)不对．