已知矩阵
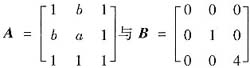 相似,则a=______,b=______.
相似,则a=______,b=______.
参考答案:3,1
解析: 方法一 因为A与B相似,所以|λE-A|=|λE-B|,利用对角线法则求行列式得
λ3-(a+2)λ2-(1+b2-2a)λ-2b+1+b2=λ3-5λ2+4λ,
比较两边同次幂的系数,得
-(a+2)=-5,-(1+b2-2a)=4,-2b+1+b2=0,
解得a=3,b=1.
方法二 因为A相似于B,而B为剥角矩阵,故知A的特征值为0,1,4,可求得
|λE-A| =λ3-(n+2)λ2-(1+b2-2a)λ-2b+1+b2.
分别令λ=0,λ=1,λ=4,得
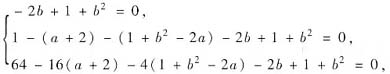
解得a=3,b=1.
方法三 利用a11+a12+a33=λ1+λ2+λ3,|A|=λ1λ2λ3,并注意A的特征值为0,1,4,得
1+a+1=0+1+4,|A|=-(b-1)2=0×1×4=0,
解得a=3,b=1.
