问题
单项选择题
已知
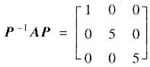，设d1是矩阵A属于特征值λ=1的特征向量，α2与α3是矩阵A属于特征值λ=5的特征向量，则矩阵P不能是
(A) (α1，-α2，α3)． (B) (α1，α2+α3，α2-2α3)．
(C) (α1，α3，α2)． (D) (α1+α2，α1-α2，α3)．
答案
参考答案：D
解析： 若
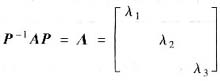，P=(α1，α2，α3)，则有AP=PΛ，即
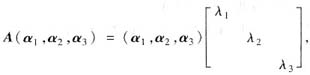
亦即 (Aα1，Aα2，Aα3)=(λ1α1，λ2α2，λ3α3)．
可见αi是矩阵A属于特征值ai的特征向量(i=1，2，3)，又因矩阵尸可逆，因此α1，α2，α3线性无关．
对于(A)：若α是属于特征值λ的特征向量，则-α仍是属于特征值λ的特征向量，故(A)正确．
对于(B)：若α，β是属于特征值λ的特征向量，则2α+3β，…仍是属于特征值λ的特征向量．本题中，α2，α3是属于λ=5的线性无关的特征向量，故α2+α3，α2-2α3仍是λ=5的特征向量，并且α2+α3，α2-2α3线性无关，故(B)正确。
对于(C)：因为α2，α3均是λ=5的特征向量，所以α2与α3准在前谁在后均正确，即(C)正确．
对于(D)：由于α1，α2是不同特征值的特征向量，因此α1+α2，α1-α2不再是矩阵A的特征向量，故(D)错误．因此应选(D)．