问题
单项选择题
设n(n≥2)阶矩阵A的行列式|A|=a≠0,λ是A的一个特征值,A*为A的伴随矩阵,则A*的伴随矩阵(A*)*的一个特征值是
(A) λ-1an-1. (B) λ-1an-2. (C) λan-2. (D) λan-1.
答案
参考答案:C
解析: 由A*A=|A|E得A*=|A|A-1.对A*应用此式,得
(A*)*=|A*(A*)-1=||A|A-1|(|A|A-1)-1
=|A|n·|A-1|(|A|-1A)=|A|n-2A=an-2A.
于是,由λ是A的一个特征值知,λan-2是(A*)*的一个特征值,故选(C).

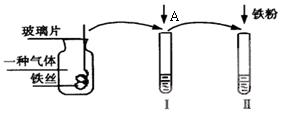
 中使用到的玻璃仪器除烧杯和漏斗外,还有________________________
中使用到的玻璃仪器除烧杯和漏斗外,还有________________________ 。
。