问题
问答题
设f(x)在(-∞，+∞)上满足对任意x，y恒有f(x+y)=e2yf(x)+f(y)cosx，又f(x)在x=0处可导，且f’(0)=1，求f(x)．
答案
参考答案：由于对任意x∈(-∞，+∞)，
由于f(x+y)=e2yf(x)+f(y)cosx，所以f(0)=0，因此
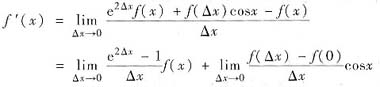
=2f(x)+f’(0)cosx=2f(x)+cosx．
从而得到f(x)满足的微分方程f’(x)-2f(x)=cosx．这是一阶线性微分方程，其通解为
记
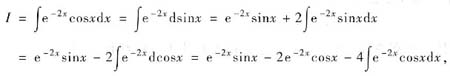
所以
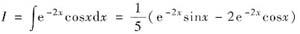
从而
．由f(0)=0，可得
，所以
