问题
问答题
已知方程(6y+x2y2)dx+(8x+x3y)dy=0的两边乘以y3f(x)后便成为全微分方程,试求出可导函数f(x),并解此微分方程.
答案
参考答案:设P(x,y)=(6y4+x2y5)f(x),Q(x,y)=(8xy3+x3y4)f(x),由
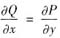 得
得
(8y3+3x3y4)f(x)+(8xy3+x3y4)f’(x)=(24y2+5x2y4)f(x).
消去y3得 16f(x)-8xf’(x)+y[2x2f(x)-x3f’(x)]=0,
有
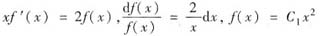
且全微分方程为
(6y4+x2y5)C1x2dx+(8xy2+x3y4)C1x2dy=0,
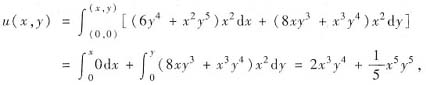
故微分方程的通解为 10x3y4+x5y5=C.