问题
填空题
设函数y1(x)，y2(x)，y3(x)是二阶线性微分方程y"+a(x)y’+b(x)y=f(x)的三个不同特解，且
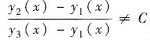，则该微分方程的通解为______．
答案
参考答案：y=y1(x)+C1[y2(x)-y1(x)]+C2[y3(x)-y1(x)]
解析： 根据线性微分方程解的叠加原理及题中条件知函数y2(x)-y1(x)和y3(x)-y1(x)都是原方程所对应的齐次方程的解．由于
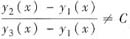，所以函数y2(x)-y1(x)和y3(x)-y1(x)线性无关．根据线性微分方程解的结构知原方程的通解为
y=y1(x)+C1[y2(x)-y1(x)]+C2[y3(x)-y1(x)]．