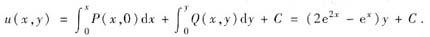问题
问答题
设f(x)二阶连续可导，且f(0)=0，f’(0)=1，求u(x，y)，使
du=y[f(x)+3e2x]dx+f’(x)dy．
答案
参考答案：
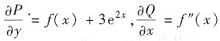，由Pdx+Qdy是u(x，y)的全微分知：
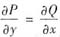，从而f"(x)-f(x)=3e2x，解此微分方程得f(x)=-ex+e2x．于是
搜题请搜索小程序“爱下问搜题”
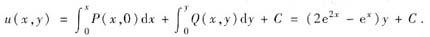
设f(x)二阶连续可导，且f(0)=0，f’(0)=1，求u(x，y)，使
du=y[f(x)+3e2x]dx+f’(x)dy．
参考答案：
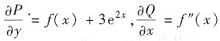，由Pdx+Qdy是u(x，y)的全微分知：
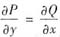，从而f"(x)-f(x)=3e2x，解此微分方程得f(x)=-ex+e2x．于是
”中，数字20是指该塔形物标的（），即自（）至（）的高度。